Advantages of 3ø Power
- The cost of utility power lines and distribution equipment per watt is about 25% less, and there is less line loss per watt.
- Three-phase motors are more efficient, are easily reversible, and any motor with a rating above 7 1/2 HP must be 3ø-phase powered.
- Multiple voltages are directly available from 3ø systems, such as 120v/208v and 277v/480v.
Disadvantages of 3ø Power
- There is a high initial-installation cost.
- Three-phase transformers can become unbalanced, causing voltages to become higher or lower than the rated value.
- The unbalanced voltages could result in severe problems for single-phase motors and equipment.
- Motor efficiency drops rapidly with a small three-phase unbalance, increasing energy cost.
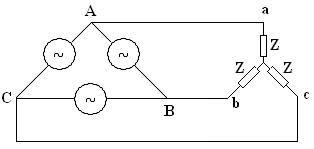
- Three-phase electrical grounding is more difficult than single phase, especially in delta-connected loads.
Common Three-Phase Voltages in the U.S.
- 120/208 for general use and for special 208 volt motors
- 277/480 used commonly in factories, mainly for motors and other devices
- 2,400/4,160 special voltage for high-horse-power motors
Distribution Voltages
- 7200/12,470 and 14,400/25,000
Transmission-Line Voltages: Delta
- 46,000/69,000 and 115,000/345,000
Voltages and Currents in Wye Three-Phase Circuits
Generators at most power plants generate three separate ac-voltage sources that are equal in voltage value but are 120 degrees out of phase with respect to each other. These voltage sources are referred to as Phase A, Phase B, and Phase C, as shown in Figure 1.
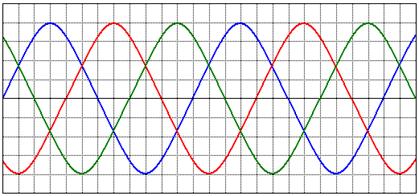
Figure 1: Phases A, B, and C of a Three-Phase System
These voltage sources are connected either in Y or in  .
.
A Y-Connected, Three-Phase System
Figure 2 shows a Y-connected, three-phase source.
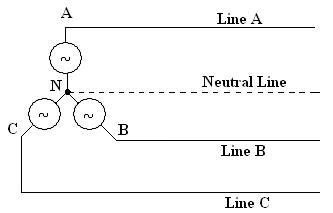
Figure 2: A Y-Connected, Three-Phase Source
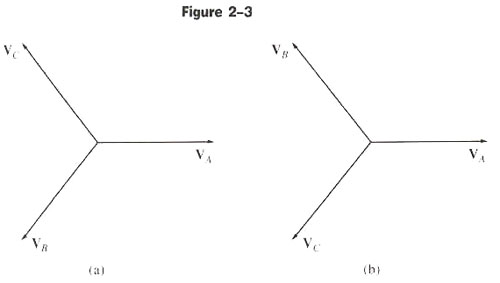
Figures 2-3a and 2-3b: Positive abc Sequence and Negative abc Sequence
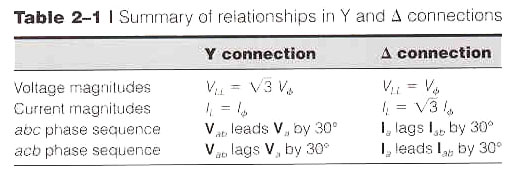
There are two standards for three-phase systems, as follows.
- Positive abc sequence
- Phase A is used as reference
- Phase B lags phase A by 120o
- Phase C leads phase A by 120o
- Negative acb sequence
- Phase A is used as reference
- Phase B leads phase A by 120o
- Phase C lags phase A by 120o
We will use only the Positive abc Standard in our discussions. For example, if
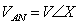 , then
, then
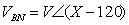 ;
;
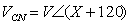 ; and
; and
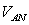 ,
, 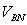 , and
, and 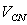 are called phase voltages.
are called phase voltages.
Example 1
The voltage between two lines is called the line-to-line voltage, such as 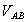 ,
, 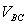 , and
, and 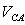 . (Note that it is
. (Note that it is 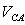 and not
and not 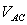 . In the abc Standard, the sequence is A, B, C, A, B, and so on. After C comes A, therefore
. In the abc Standard, the sequence is A, B, C, A, B, and so on. After C comes A, therefore 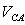 .)
.)
To determine line-to-line voltages (VLL), we multiply the magnitude of phase voltages (V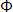 ) by
) by 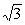 and add 30o to the corresponding phase angles.
and add 30o to the corresponding phase angles.
Notice that EAN - EBN is shown vectorally in the diagram above.
Example 2
If 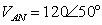 , determine all the line-to-line voltages.
, determine all the line-to-line voltages.
From Example 1
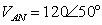 →
→ 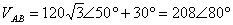
Once we determine 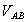 , we can determine
, we can determine 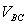 and
and 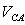 using the rules of the abc sequence.
using the rules of the abc sequence.
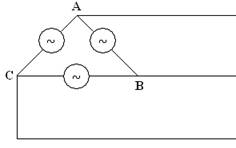
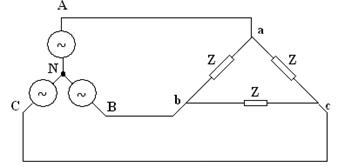
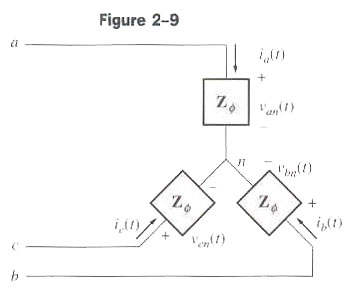
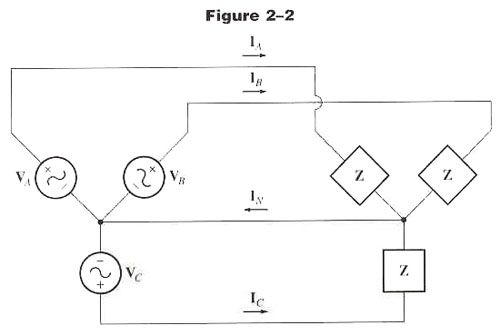
We now connect our three-phase source to a three-phase balanced load, with each load having impedance Z, as shown in Figure 3.
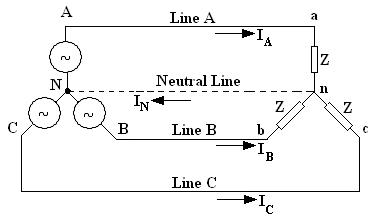
Figure 3: A Y-Y Connected, Three-Phase System
This is called a Y-Y connected source load.
Line currents are determined by solving simple individual circuits.
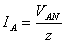
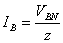
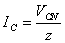
Example 3
For the problem in Example 2, determine the line currents if the impedance of each phase is 25 .
.
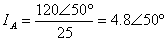
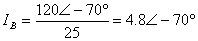
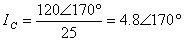
Example 4
For the problem in Example 3, determine IN.
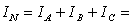 ,
, 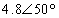 +
+ 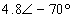 +
+ 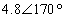 =0
=0
The result may sound surprising, but the fact is that the return current to the three-phase source is 0 if the load is balanced.
 Three-phase power is the preferred type of electrical energy for most of the power transmissions in the world. This week, we will explore three-phase power, its advantages and disadvantages, and go through the math. We will also help you understand some basic parameters about three-phase power. Note that, in three-phase systems, there is not an instance in time when the output voltage is 0.
Three-phase power is the preferred type of electrical energy for most of the power transmissions in the world. This week, we will explore three-phase power, its advantages and disadvantages, and go through the math. We will also help you understand some basic parameters about three-phase power. Note that, in three-phase systems, there is not an instance in time when the output voltage is 0.
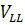
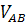 .
.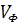
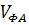 .
.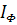
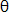
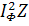 cos
cos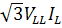 cos
cos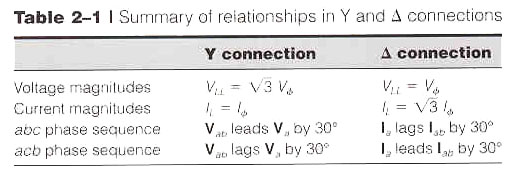
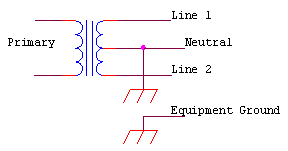 120 Volt Single Phase (Single-Phase Two Wire)
120 Volt Single Phase (Single-Phase Two Wire)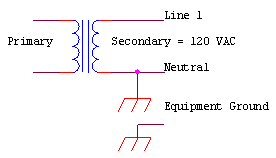 120/240 Volt Single Phase (Single-Phase Three Wire)
120/240 Volt Single Phase (Single-Phase Three Wire)


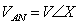 , then
, then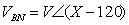 ;
;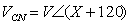 ; and
; and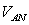 ,
, 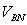 , and
, and 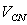 are called phase voltages.
are called phase voltages.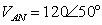
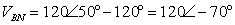
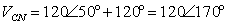
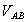 ,
, 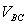 , and
, and 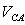 . (Note that it is
. (Note that it is 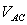 . In the abc Standard, the sequence is A, B, C, A, B, and so on. After C comes A, therefore
. In the abc Standard, the sequence is A, B, C, A, B, and so on. After C comes A, therefore 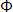 ) by
) by 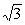 and add 30o to the corresponding phase angles.
and add 30o to the corresponding phase angles.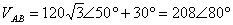
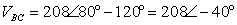
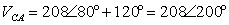

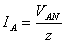
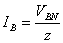
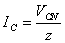
 .
.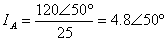
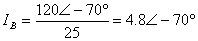
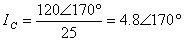
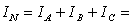 ,
, 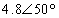 +
+ 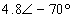 +
+ 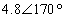 =0
=0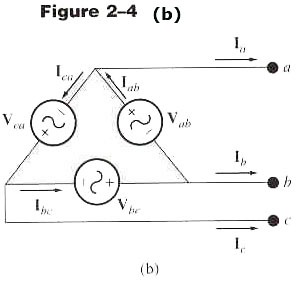
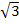 and add 30o to the corresponding phase angles.
and add 30o to the corresponding phase angles.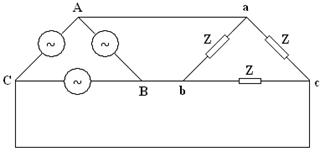

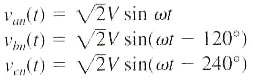 Then the phase currents are as follows.
Then the phase currents are as follows.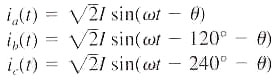
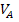 =
= 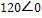 , and the phase is abc. Find
, and the phase is abc. Find 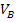 ,
, 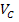 ,
, 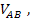
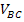 ,
, 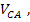
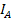 ,
, 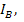
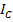 , and
, and 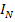 if Z is 30 ohms. Find the total real, reactive, and apparent power.
if Z is 30 ohms. Find the total real, reactive, and apparent power.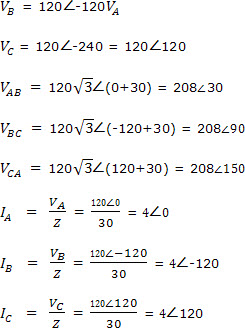
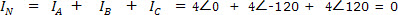 , which is correct for a balanced system.
, which is correct for a balanced system.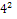 * 30 cos0 = 1.44kw
* 30 cos0 = 1.44kw